《算法导论》ITA（一）归并排序

• 时间复杂度：O(nlogn)
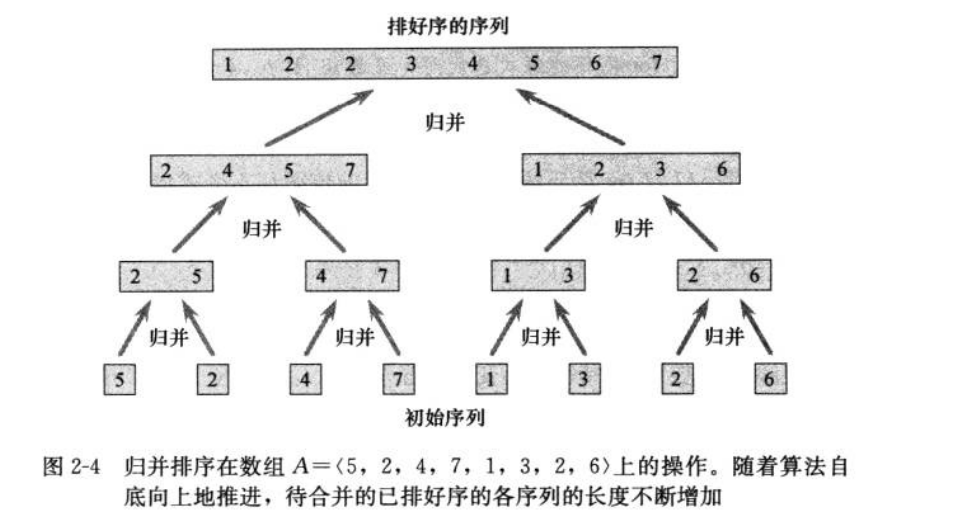
• 归并排序完全遵循分治模式，直观上操作如下
  • 分解：分解待排序的n个元素的序列成各具n/2个元素的两个子序列
  • 解决：使用归并排序递归排序两个子序列
  • 合并：合并两个已排序的子序列以产生已排序的答案
• 在子序列元素个数为1时直接返回

代码如下：

#include<stdio.h>
#include<stdlib.h>
#define maxn 1000000

// 待排序数组a，临时数组tmp
void merge_sort(int *a, int l, int r, int *tmp) {
    if (l == r) return;
    if (l < r) {
        int mid = l + r >> 1;
        //递归处理序列左右两段
        merge_sort(a, l, mid, tmp); 
        merge_sort(a, mid + 1, r, tmp);
        //将两段有序序列合并
        //将将合并的序列放在临时数组tmp中
        int i = l, j = mid + 1, k = l;
          while (i <= mid || j <= r) {
              //处理一段序列已经空了的情况
              if (i > mid) {
                  tmp[k ++] = a[j];
                  j ++;
                  continue;
              }
              if (j > r) {
                  tmp[k ++] = a[i];
                  i ++;
                  continue;
              }
              //处理两段数列都非空的情况
              if (a[i] <= a[j]) {
                  tmp[k ++] = a[i];
                  i ++;
              }
              else {
                  tmp[k ++] = a[j];
                  j ++;
              }
          }
          //将临时数组tmp中的数据放回序列数组a中
          for (-- k; k >= l; -- k) a[k] = tmp[k];
    }
}

int main() {
    int i, n;
    scanf("%d", &n);
    int *a = malloc(sizeof(int) * n);
    int *tmp = malloc(sizeof(int) * n);
      if (a == NULL || tmp == NULL) return 0;
      for (i = 0; i < n; ++ i) scanf("%d", &a[i]);
    merge_sort(a, 0, n - 1, tmp);
      for (i = 0; i < n; ++ i) printf("%d ", a[i]);
    return 0;
}