《深入理解计算机系统》CSAPP(二)
信息的表示和处理
- 无符号编码
- 表示≥0的数字
- 补码编码
- 表示有符号整数
- 浮点数编码
- 表示实数的科学计数法的以2为基数的版本
- 溢出
- 计算机以有限位表示结果
- 结果过大不能表示导致溢出
- 如$200 \times 300 \times 400 \times 500 = -884901888$
- 整数的计算机运算满足真正整数运算的许多性质
- 如乘法满足结合律和交换律
- 浮点运算
- 溢出产生特殊值+∞
- 一组正数的乘积总是正的
- 不可结合
- $3.14 + (10^{20} - 10^{20}) = 3.14$
- $(3.14 + 10^{20}) - 10^{20} = 0$
- 整数编码虽然只能编码一个较小的范围,但表示精确
- 浮点数编码虽然可以编码一个较大的范围,但表示近似
信息存储
十六进制表示法
- 用十六进制(hex)来表示值
- ‘0’ $\sim$ ‘9’,‘A’ $\sim$ ‘F’,表示16个值
- C语言中以0x或0X开头
- 熟悉十六进制,十进制和二进制之间的相互转化
字数据大小
- 每台计算机都有一个字长,指明指针数据的标称大小
- 虚拟地址以这样的一个字来编码$\rightarrow$字长决定的最重要的系统参数就是虚拟地址空间的最大大小
- 对一个字长为w位的机器而言,虚拟地址的范围为$0 \sim 2^{w}-1$,程序最多访问$2^{w}$个字节
大多数64位机器可以运行32位机器编译的程序,这是一种向后兼容
当程序prog.c用如下伪指令编译后
linux> gcc -m32 prog.c
该程序可以在32位或64位机器上正确运行
用下述伪指令编译后
linux> gcc -m64 prog.c
就只能在64位机器上运行
- 将程序称为“32位程序”或“64位程序”时,区别在于该程序是如何编译的,而不是其运行的机器类型
- 计算机和编译器支持多种不同方式编码的数字格式
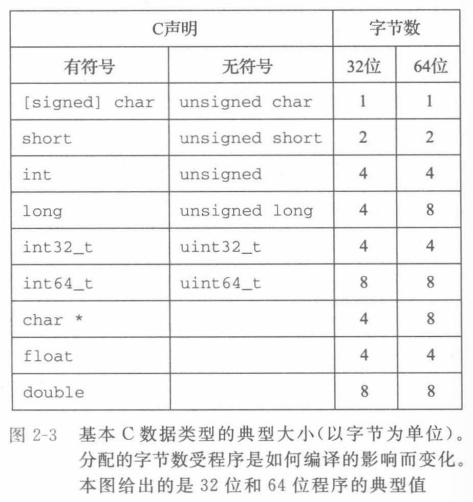
- C语言标准对不同数据类型的数字范围设置了下界,但是却没有上界
寻址和字节顺序

- 大多数intel机都只用小端模式
- 双端法
- 既可以配置成大端也可以配置成小端
- 但一旦选定了操作系统,其字节顺序就固定了
- 书写字节序列时最低位字节在左边,最高位字节在右边
- C语言中可通过强制类型转换或联合来允许一种数据类型引用一个对象,而这种数据类型与创建这个对象时定义的数据类型不同
- 用浮点型和整型表示同一个数据时,将十六进制转化为二进制后,并进行适当的移位,就会发现一个有13个相匹配的位的序列。
- 如下图,分别用整型和浮点型表示12345

- 而这并不是巧合,我们后面会进行相关学习
表示字符串
- C语言中字符串被编码为一个以NULL字符结尾的字符数组
- 文本数据比二进制数据具有更强的平台独立性
表示代码
1 | int sum(int x, int y) { |
- 编译上述代码时,在不同机器上生成的机器代码如下

- 发现指令编码不同
- 不同机器类型使用不同且不兼容的指令和编码方式
- 二进制代码不兼容
布尔代数简介
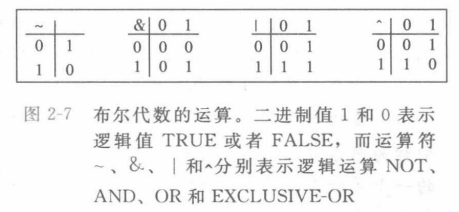

C语言中的位级运算
- C语言支持按位布尔运算
- 位运算实现掩码运算
C语言中的逻辑运算
- 逻辑运算符
- ||、&&、!
- 如果对第一个参数求值就能确定表达式的值,那么逻辑运算符就不会对第二个参数求值
- a && 5 / a 不会造成被零除
- p && *p++也不会导致间接引用空指针
- 不要混淆逻辑运算和位运算
C语言中的移位运算
- 左移
- <<
- x << k
- 右端补k个0
- 右移
- >>
- x >> k
- 机器支持逻辑右移和算术右移
- 逻辑右移
- 左端补k个0
- 算术右移
- 左端补k个最高有效位的值
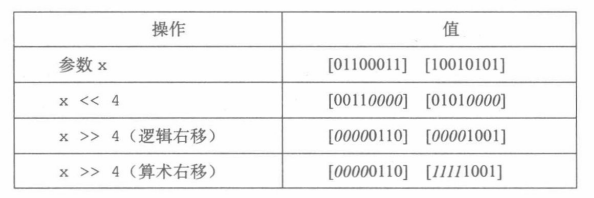
- 左端补k个最高有效位的值
- C语言中几乎所有编译器都对有符号数使用算术右移,对无符号数进行逻辑右移

- 注意移位运算的优先级!
整数表示
- 相关的数学术语
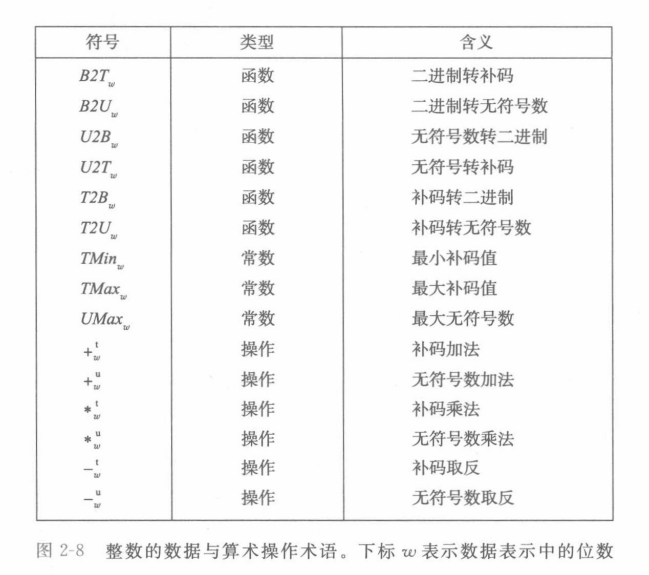
整数数据类型
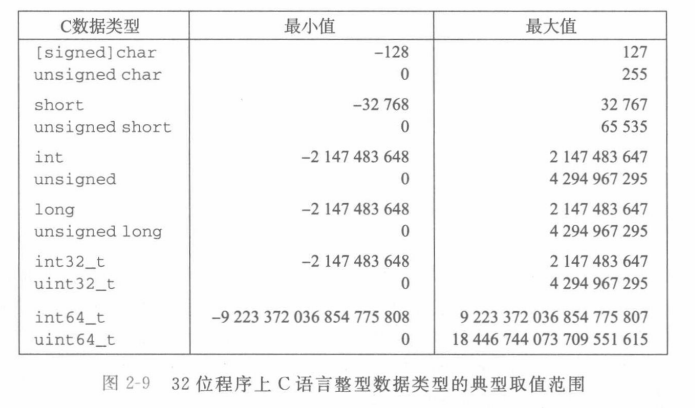
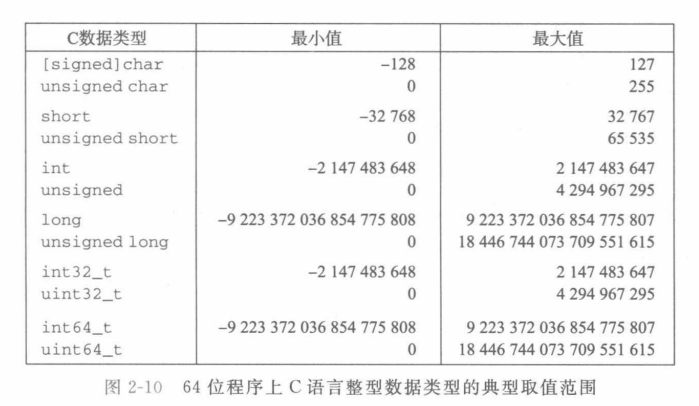
- 取值范围不对称
- 负数范围比正数范围大1
- C语言标准定义了每种数据类型必须能够表示的最小的取值范围
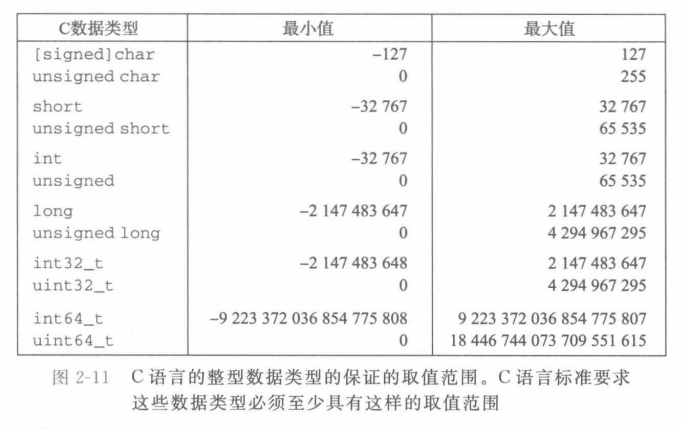
无符号数的编码
- 无符号数编码的定义
- 对向量$\vec{x}=[x_{w-1},x_{w-2},…,x_{0}]:$
- 如$B2U_4([0101])=0\cdot2^3+1\cdot2^2+0\cdot2^1+1\cdot2^0=0+4+0+1=5$
- $0~2^w-1$
- 编码具有唯一性
补码编码
- 最高有效位解释为负权
- 补码编码的定义
- 向量$\vec{x}=[x_{w-1},x_{w-2},…,x_{0}]:$
- 最高有效位$x_{w-1}$也称为有效位
- 他为1时,表示值为负
- 他为0时,表示值为正
- 如$B2U_4([0101])=-0\cdot2^3+1\cdot2^2+0\cdot2^1+1\cdot2^0=0+4+0+1=5$
- $B2U_4([1011])=-1\cdot2^3+0\cdot2^2+1\cdot2^1+1\cdot2^0=-8+0+2+1=-5$
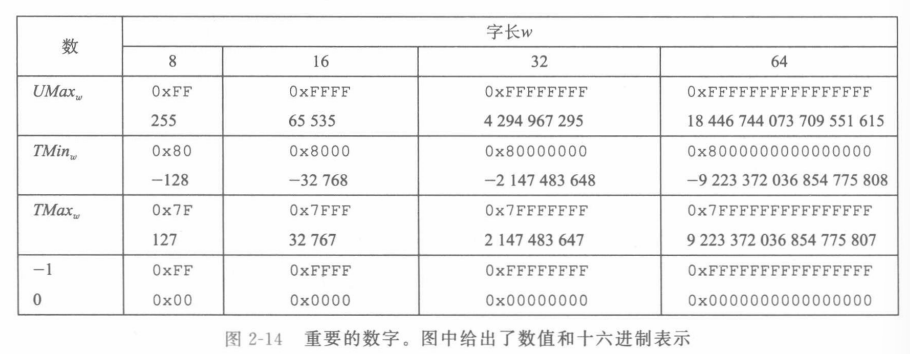
- 表示最小值的向量为[10…0],值为$-2^{w-1}$
- 最大值的向量为[011…1],值为$2^{w-1}-1$
- $-2^{w-1}~2^{w-1}-1$
- 补码具有唯一性
- 注意事项
- 补码范围不对称:|TMin|=|TMax|+1
- 最大无符号数值刚好比补码的最大值的两倍大1:$UMax_w=2TMax_w+1$
- 几乎所有现代机器都使用补码
有符号数的其他表示方法
- 反码
- 除了最高有效位的权为$-(2^{w-1}-1)$而不是$-2^{w-1}$,他和补码是一样的
- 原码
- 最高有效位是符号位,用来确定剩下的位应该取负权还是正权
- 这两种方法都有一个奇怪的属性
- 把[00…0]都解释为+0
- -0在反码中表示为[11…1],在原码中表示为[10…0]
有符号数和无符号数之间的转换
- C语言允许各种不同的数字数据类型之间做强制类型转换
- 强制类型转换的结果保持位置不变,只是改变了解释这些位的方式
C语言中的有符号数与无符号数
- 要创建一个无符号常量,必须加上后缀字符’U’或者’u’
- 如12345U或者0x5A11u
- 如果无符号和有符号的数同时参与运算,C语言会将无符号强制转换为有符号
- 这会导致非直观的影响
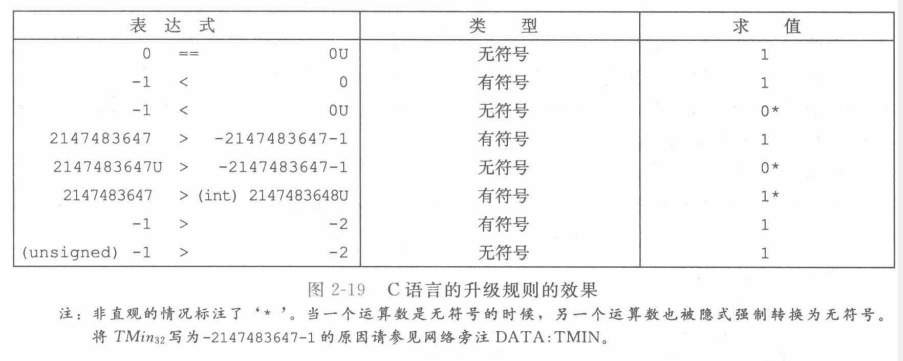
- 这会导致非直观的影响
扩展一个数字的位表示
- 无符号数的零扩展
- 定义宽度为w的位向量$\vec{u}=[u_{w-1},u_{w-2},…,u_0]$和宽度位$w^{‘}$的位向量$\vec{u^{‘}}=[0,…,0,u_{w-1},u_{w-2},…,u_0]$,其中$w_{‘}>w$。
- 则$B2U_w(\vec{u})=B2U_{w^{‘}}(\vec{u^{‘}})$
- 补码数的符号扩展
- 定义宽度为w的位向量$\vec{x}=[x_{w-1},x_{w-2},…,x_0]$和宽度位$w^{‘}$的位向量$\vec{x^{‘}}=[x_{w-1},…,x_{w-1},x_{w-1},x_{w-2},…,x_0]$,其中$w_{‘}>w$。
- 则$B2T_w(\vec{x})=B2T_{w^{‘}}(\vec{x^{‘}})$
- 当把short转换成unsigned时,要先改变大小,再完成有符号到无符号的转换
截断数字
- 减少表示一个数字的数位时会发生截断
- 从高位进行截断
整数运算
无符号加法
- 若相加没有溢出,则正常相加运算
- 若发生溢出,则进行高位截断
- 对满足$0≤x,y<2^w$的x和y有:
- 无符号数求反
- 对满足$0≤x<2^w$的任意x,其w位的无符号逆元$-^{u}_{w}x$,由下式给出:
- 对满足$0≤x<2^w$的任意x,其w位的无符号逆元$-^{u}_{w}x$,由下式给出:
补码加法
- 若相加没有溢出,则正常相加运算
- 若发生溢出,则进行高位截断
- 对满足$-2^{w-1}≤x,y≤2^{w-1}-1$的整数x和y,有:
补码的非
- 对满足$TMin_w≤x≤TMax_w$的x,其补码的非$-_{w}^{t}x$为
无符号乘法
- 对满足$0≤x,y≤UMax_w$的x和y有:
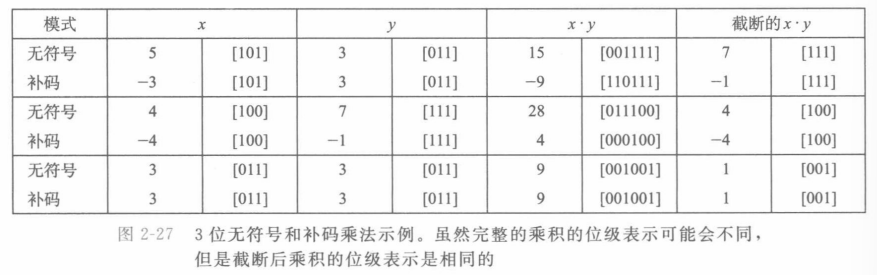
补码乘法
- 仍然是相乘后高位截断
- 对满足$TMin_w≤x,y≤TMax_w$的x和y有:
乘以常数
- 整数乘法指令相当慢
- 因此,编译器试着使用移位和加法运算的组合来代替乘以常数因子的乘法
- 左移k位表示乘以$2^k$
- 对固定字长左移k位时,其高k位被丢弃,相当于无符号乘法
- 编译器会将x*14改写为(x<<3)+(x<<2)+(x<<1)或(x<<4)-(x<<1)

除以2的幂
- 整数除法甚至比整数乘法更慢
- 用右移和加法运算组合来代替
- 无符号和补码数分别使用逻辑移位和算术移位来实现
- 对x≥0,y>0,结果为$\lfloor x/y \lfloor$
- 对x<0,y>0,结果$\lceil x/y \rceil$
- 向下舍入一个正值,向上舍入一个负值
- 无符号数直接进行右移即可,但补码数直接右移会导致向下舍入
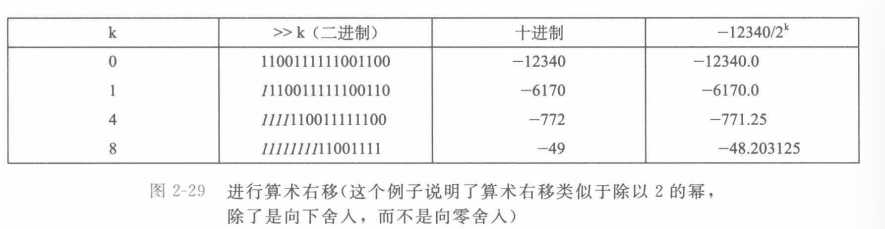
- 在执行算术右移之前加上一个适当的偏置量来导致结果正确舍入
- C变量x和k分别有补码值x和无符号数值k,且0≤k< w,则当执行算数移位时,C表达式(x+(1<< k)-1)>>k产生数值$\lceil x/y \rceil$

- 同乘法不同, 不能用除以2的幂的除法来表示除以任意常数k的除法
浮点数
- 对形如V=$x \times 2^y$的有理数进行编码。
- 用于非常大的数字(|V|>>0)、非常接近0(|V|<<1)的数字,以及实数运算的近似值计算
二进制小数
- $b=b_{m}b_{m-1}…b_{1}.b_{-1}b_{-2}…b_{-n-1}b_{-n}$
- $b=\sum_{i=-n}^{m}2^{i} \times b_{i}$
IEEE浮点表示
- IEEE浮点标准用V=$(-1)^s \times M \times 2^E$的形式来表示一个数
- 符号s决定这数是负数(s=1)还是正数(s=0),而对于数值0的符号位解释作为特殊情况处理
- 尾数M是一个二进制小数,它的范围是1$\sim$-ε,或者是0$\sim$1-ε
- 阶码E的作用是对浮点数加权,这个权重是2的E次幂(可能是负数)。
- 将浮点数的位表示划分为三个字段,分别对这些值进行编码:
- 一个单独的符号位s直接编码符号s
- n位小数字段frac=$f_{n-1}…f_1f_o$编码尾数M,但是编码出来的值也依赖于阶码字段的值是否等于0
- k位的阶码字段exp=$e_{k-1}…e_1e_0$编码阶码E

- 根据exp的值,被编码的值可以分为三种不同的情况
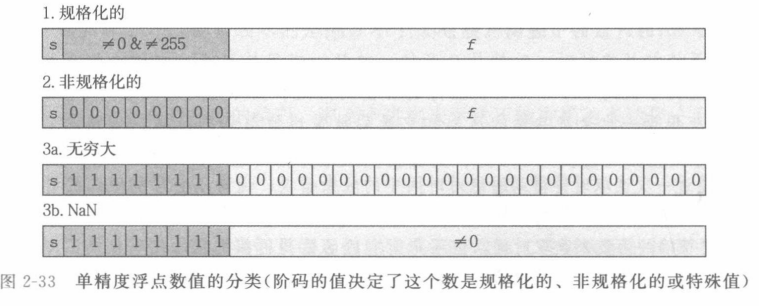
- 规格化的值
- 当exp的位模式既不全为0,也不全为1时
- E=e-Bias,e是无符号数,位表示为$e_{k-1}…e_1e_0$,Bias为一个等于$2^{k-1}-1$的偏置值
- M=1+f,1≤M<2
- 非规格化的值
- 阶码域全为0时
- E=1-Bias
- M=f
- 提供了一种表示数值0的方法
- 由于符号位的存在,+0.0与-0.0被认为是不同的
- 用于表示非常接近与0.0的数
- 逐渐溢出:可能的数值分布均匀地接近于0.0
- 特殊值
- 阶码全为1时
- 当小数域全为0时,得到的值表示无穷
- s=0时为+∞,s=1时为-∞
- 无穷能表示溢出的结果
- 运算结果不能是实数或无穷,返回NaN(Not a Number)
- 规格化的值
数字示例
舍入
- 浮点数无法准确表示,需要进行舍入
- 四种舍入方法
- 向偶数舍入
- 向零舍入
- 向下舍入
- 向上舍入
- 当数字不是两个可能值的正中间时,利用类四舍五入法判断使用向上舍入还是向下舍入
- 如舍入到四分之一时,$10.00011_2$向下舍入为$10.00_2$,$10.00110_2$向上舍入为$10.01_2$
- 当数字位于两个可能值的正中间时,采用向偶数舍入,舍得末位为0
- 如舍入到四分之一时,$10.11100_2$向上舍入为$11.00_2$,$10.10100_2$向下舍入为$10.10_2$
浮点运算
- 浮点加法可交换
- x + y = y + x
- 浮点加法不具有结合律
- 3.14 + (1e10 - 1e10) = 3.14
- (3.14 + 1e10) - 1e10 = 0
- 浮点加法具有单调性
- 如果x≥y,则对于任意x,y以及a的值(除了NaN),都有x+a≥y+a
- 无符号或补码加法不具有此性质
- 浮点乘法可交换
- x * y = y * x
- 浮点乘法不具有结合律
- (1e20 * 1e20) * 1e-20 = +∞
- 1e20 * (1e20 * 1e-20) = 1e20
- 浮点乘法在加法上不具有分配性
- 1e20 * (1e20 - 1e20) = 0.0
- 1e20 * 1e20 - 1e20 * 1e20 = NaN
- 浮点乘法具有单调性
C语言中的浮点数
- float和double分别对应单精度和双精度浮点

- 必须小心地使用浮点运算,注意整型和浮点型之间的转换!
《深入理解计算机系统》CSAPP(二)
